http://poj.org/problem?id=2663
用1 x 2的多米诺骨牌填满M x N的矩形有多少种方案,M<=5,N<2^31,输出答案mod p的结果.
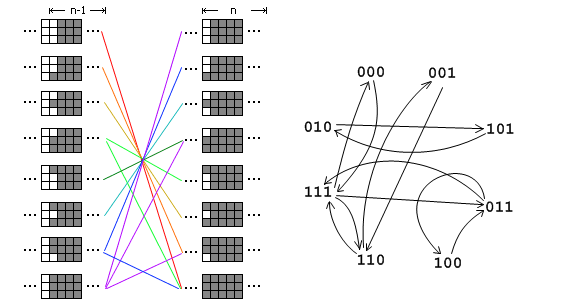
我们以M=3为例进行讲解。假设我们把这个矩形横着放在电脑屏幕上,从右往左一列一列地进行填充。其中前n-2列已经填满了,第n-1列参差不齐。现在我 们要做的事情是把第n-1列也填满,将状态转移到第n列上去。由于第n-1列的状态不一样(有8种不同的状态),因此我们需要分情况进行讨论。在图中,我 把转移前8种不同的状态放在左边,转移后8种不同的状态放在右边,左边的某种状态可以转移到右边的某种状态就在它们之间连一根线。注意为了保证方案不重 复,状态转移时我们不允许在第n-1列竖着放一个多米诺骨牌(例如左边第2种状态不能转移到右边第4种状态),否则这将与另一种转移前的状态重复。把这8 种状态的转移关系画成一个有向图,那么问题就变成了这样:从状态111出发,恰好经过n步回到这个状态有多少种方案。比如,n=2时有3种方 案,111->011->111、111->110->111和111->000->111,这与用多米诺骨牌覆盖 3x2矩形的方案一一对应。这样这个题目就转化为了我们前面的例题8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
| #include<stdio.h>
#include<cstring>
#include<algorithm>
#include<iostream>
#define mem(x,y) memset(x,y,sizeof(x))
#define inf 0x3f3f3f3f
using namespace std;
#define siz 6
#define Mytype int
int N=6;
Mytype mod = 1000;
struct matrix
{
Mytype a[siz][siz];
matrix operator*(const matrix &y)const
{
matrix res;
mem(res.a,0);
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
if(a[i][j])
for(int k=0;k<N;k++)
res.a[i][k]+=a[i][j]*y.a[j][k];
return res;
}
matrix operator+(const matrix &y)const
{
matrix res;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
res.a[i][j]=a[i][j]+y.a[i][j],res.a[i][j]%=mod;
return res;
}
matrix operator*=(const matrix &y)
{
*this=y* *this;
return *this;
}
};
matrix qmod(matrix a,int k)
{
matrix res;
mem(res.a,0);
for(int i=0;i<N;i++)
res.a[i][i]=1;
while(k)
{
if(k&1)
res*=a;
a*=a;
k>>=1;
}
return res;
}
int ans[35];
int main()
{
matrix a;
mem(a.a,0);
a.a[4][1]=1;
a.a[3][2]=1;
a.a[5][2]=1;
a.a[2][3]=1;
a.a[1][4]=1;
a.a[5][4]=1;
a.a[0][5]=1;
a.a[2][5]=1;
a.a[4][5]=1;
a.a[5][0]=1;
matrix res=a;
for(int i=0;i<=30;i++)
{
ans[i]=res.a[0][5];
res*=a;
}
int n;
while(scanf("%d",&n),~n)
printf("%d\n",ans[n]);
}
|
EOF
